Week 2 - Exercise#
Problem Statement#
A perfectly mixed gas permeation module is used to separate carbon dioxide from nitrogen using a poly (2,6-dimethylphenylene oxide) membrane (\(P_{CO_2}=0.034\times10^{-13}\) \(P_{N_2}=0.089\times10^{-14} [cm^3 (STP) / cm s Pa]\)). The process carried out at a temperature of 25\(^oC\). The feed flowrate is 20.0 mol% carbon dioxide. The module has 15.0 \(m^2\) of membrane. The module is operated with a retentate pressure of 5.5 atm and a permeate pressure of 1.01 atm.
The permeate is enriched to 38.0 mol% in carbon dioxide. The membrane thickness is \(\ell = 2.0 \times 10^{-4}\) cm.
Draw a scheme of the unit clearly labelling all the streams and relevant variables.
Completely characterise the unit, by computing feed, permeate and retentate flow rates, cut, and retentate composition.
Solution trace#
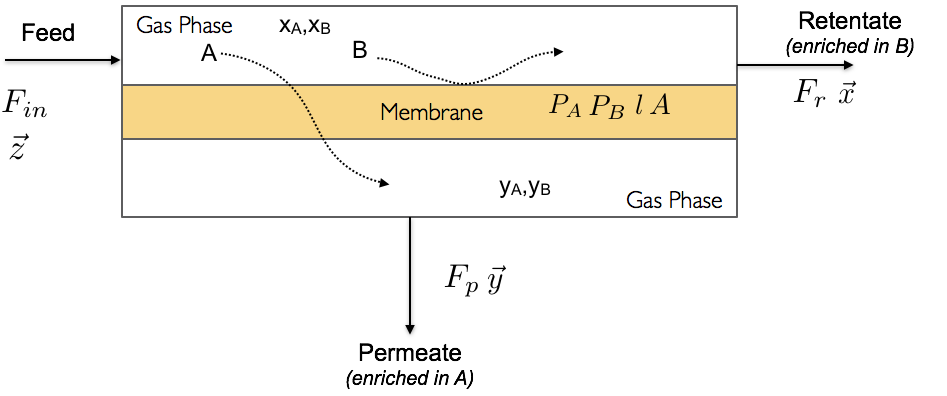
Schematics of a membrane process with all variables defined.#
Unknowns: \(x\),\(F_{p}\),\(F_{in}\), \(F_{r}\), \(\theta\)
We can start computing the ideal separation factor and the composition in the retentate:
and then using the rate transfer equation to computing \(x\):
Then we can compute the cut:
and the permeate flowrate from the flux equation:
where \(\rho_{STP}\) is the molar density of an ideal gas at standard T and P.
Finally, the retentate flowrate can be computed as:
## Solution trace
# Variables
A=15 * 1E4 # [m^2 * cm^2 / m^2]
P_r=5.5 * 101325 # [atm] * [Pa / atm]
P_p=1.01 * 101325 # [atm] * [Pa / atm]
l=2.0*1E-4 # cm
rho_STP=1/22.4E3 # / [mol/cm3(stp)]
PCO2=0.034E-13 * 3600 # [cm3(STP) * cm/cm2/s/Pa] * [s/h]
PN2=0.089E-14 * 3600# [cm3(STP) * cm/cm2/s/Pa] * [s/h]
# Permeate Composition
y=0.38
# Feed Composition
z = 0.20
# 1. compute the retentate composition:
alpha=PCO2/PN2
x= y * (1 + P_p/P_r * (1-y) * (alpha - 1)) / (alpha - (alpha - 1) * y)
# 2. compute the cut:
theta=(z-x)/(y-x)
# 3. compute the permeate flowrate:
Fp=A*PCO2*rho_STP / y / l * (x*P_r-y*P_p)
# 4. compute the feed flowrate:
Fin=Fp/theta
# 5 compute the retentate flowrate:
Fr=Fin-Fp
print("\nRetentate composition: ", f"{x:.4}", " [-]")
print("Cut: ", f"{theta:.4}", "[-]")
print("Permeate flowrate: ", f"{Fp:.4}", " [mol/h]")
print("Feed flowrate: ", f"{Fin:.4}", " [mol/h]")
print("Retentate flowrate: ", f"{Fr:.4}", " [mol/h]\n")
Retentate composition: 0.1826 [-]
Cut: 0.08792 [-]
Permeate flowrate: 0.06784 [mol/h]
Feed flowrate: 0.7715 [mol/h]
Retentate flowrate: 0.7037 [mol/h]
The brute force way
## Solution trace
import scipy as sp
##from sp.optimize import fsolve
# Variables
A=15 * 1E4 # [m^2 * cm^2 / m^2]
P_r=5.5 * 101325 # [atm] * [Pa / atm]
P_p=1.01 * 101325 # [atm] * [Pa / atm]
l=2.0*1E-4 # cm
rho_STP=1/22.4E3 # / [mol/cm3(stp)]
PCO2=0.034E-13 * 3600 # [cm3(STP) * cm/cm2/s/Pa] * [s/h]
PN2=0.089E-14 * 3600# [cm3(STP) * cm/cm2/s/Pa] * [s/h]
# Permeate Composition
y=0.38
# Feed Composition
z = 0.20
alpha=PCO2/PN2
def equations(vars):
x, Fin, Fp, Fr, theta = vars
eq1 = ((theta - 1) / theta) * x + (z / theta) - y
eq2 = x - (y * (1 + P_p/P_r * (1-y) * (alpha - 1)) / (alpha - (alpha - 1) * y))
eq3 = Fin - Fr - Fp
eq4 = Fp-A*PCO2*rho_STP / y / l * (x*P_r-y*P_p)
eq5 = Fin - (Fp/theta)
return [eq1, eq2, eq3, eq4, eq5]
x, Fin, Fp, Fr, theta = sp.optimize.fsolve(equations, (0.1, 0.1, 0.1, 0.1, 0.1))
print("\nRetentate composition: ", f"{x:.4}", " [-]")
print("Cut: ", f"{theta:.4}", "[-]")
print("Permeate flowrate: ", f"{Fp:.4}", " [mol/h]")
print("Feed flowrate: ", f"{Fin:.4}", " [mol/h]")
print("Retentate flowrate: ", f"{Fr:.4}", " [mol/h]\n")
Retentate composition: 0.1826 [-]
Cut: 0.08792 [-]
Permeate flowrate: 0.06784 [mol/h]
Feed flowrate: 0.7715 [mol/h]
Retentate flowrate: 0.7037 [mol/h]
Contributions#
Divyansh Vashishtha, 19 Feb 2024
