Week 5 - Exercise#
Problem Statement#
A protein mixture has been separated through an ion-exchange chromatography process. The residence time of the column in non-adsorbing conditons is \(t_0=1\) min. The chromatogram resulting from the separation is reported in the following:
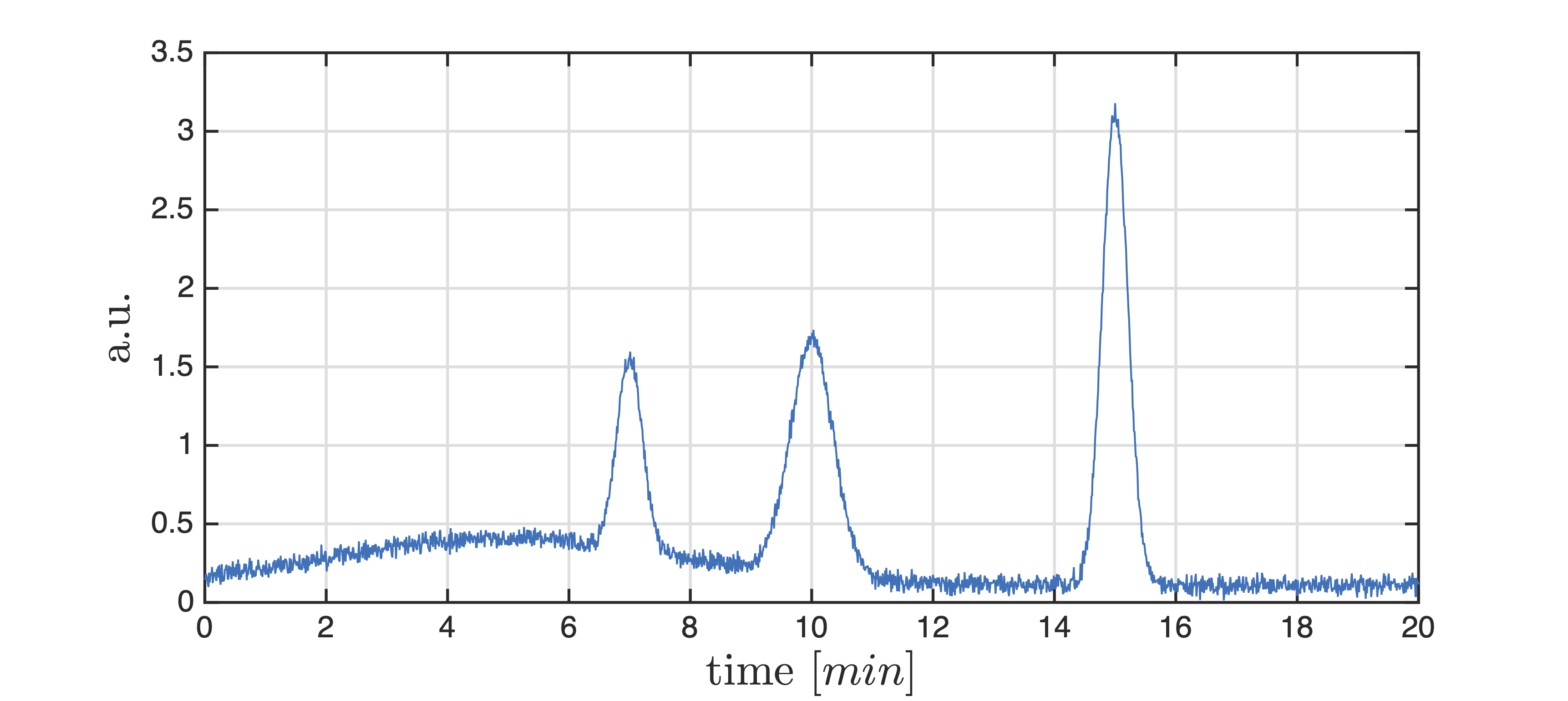
Fig. 5 Experimental chromatogram.#
Determine:#
How many components in the mixture can you identify from the chromatogram?
What is the selectivity of this column for each couple of components?
Assuming a linear adsorption isotherm holds in all cases, what conclusions can you draw about adsorption thermodynamics of each component in the column?
What is the number of theoretical plates associated to the elution of each component you have identified? If the coulmn is 10 cm long, what is the height equivalent of a theoretical plate for each component of the mixture?
Compute the resolution relative to each couple of components in the chromatogram. Does it depend only on the adsorption thermodynamics?
Comment on the separation performances of the column. Does it allow for a sharp resolution of all components?
Solution#
The chromatogram clearly indicates three components, let us indicate them with A, B, and C. The retention times for these components are:
\(t_{r,A}=7\)
\(t_{r,B}=10\)
\(t_{r,C}=15\)
The selectivity can be computed for every pair of components as:
import numpy as np
tr=np.array([7,10,15]);
t0=1
SEL=np.zeros((np.size(tr),np.size(tr)));
for i in range(0,np.size(tr)):
for j in range(0,np.size(tr)):
SEL[i,j]=(tr[i]-t0)/(tr[j]-t0)
print('Selectivity i,j\n',SEL)
Selectivity i,j
[[1. 0.66666667 0.42857143]
[1.5 1. 0.64285714]
[2.33333333 1.55555556 1. ]]
Since \(S_{i,j}=H_i/H_j\) we can determine the relative affinity of components A, B and C for the startionary phase. Component C shows the highest affinity for the stationary phase, followed by B and then C.
4/5. The number of theoretical plates associated to the elution of components A, B, and C can be obtained applying the relationship \(N=16*(tr/tw)^2\). The resolution for every couple of components is computed as: \(R_{i,j}=\frac{t_{r,i}-t_{r,j}}{\frac{1}{2}(t_{w,i}+t_{w,j})}\)
import numpy as np
tr=np.array([7,10,15]);
tw=np.array([1,2,1.5]);
L=10 #cm
N=(16*(tr/tw)**2)
H=L/N
R=np.zeros((np.size(tr),np.size(tr)));
for i in range(0,np.size(tr)):
for j in range(0,np.size(tr)):
R[i,j]=abs((tr[i]-tr[j])/(2*(tw[i]+tw[j])))
print('\nHeight of a theoretical plates ',H,' [-]')
print('Number of theoretical plates ',H,' cm')
print('Resolution i,j\n',R)
Height of a theoretical plates [0.0127551 0.025 0.00625 ] [-]
Number of theoretical plates [0.0127551 0.025 0.00625 ] cm
Resolution i,j
[[0. 0.5 1.6 ]
[0.5 0. 0.71428571]
[1.6 0.71428571 0. ]]
