6. The BET Isotherm

The BET (Brunauer, Emmet and Teller) isotherm allows to extend ideas and hypotheses that are adopted to obtain the Langmuir isotherm to describe the adsorption of a component from a gas phase in cases in which it can form multiple layers on the surface of the stationary phase, up to the limit in which it condenses into a macroscopic liquid phase.

The hypotheses at the foundation of the BET theory are:

• Lateral interactions between adsorbed molecules (i.e. interactions between molecules adsorbed in the same layer) are neglibile. In other words the adsorption process does not depend on the local environment around an adsorption site. This hypothesis is common to the derivation of the Langmuir isotherm.

• Molecules can adsorb in an infinite number of layers.

• The adsorption enthalpy on the first layer is constant and independent from the fractional occupation of that layer.

• The adsorption enthalpy in layers from the second onwards is constant and corresponds to the condensation enthalpy.

Following an approach similar to the one adopted for the derivation of the Langmuir isotherm let us begin by defining the rates of adsorption and desorption. In the case of th BET isotherm the rates will depend on the layer considered and will therefore have subscript \(i\) that indicate the layer on which adsorption takes place.

The adsorption rate on layer \(i\) can be written as:

(65)\[ R_{A,i}=k_{A,i}\Gamma_iP \]

The desorption rate instead, explicitly introducing the dependence on the adsorption enthalpy through an Arrhenius-like functional form, is written as:

(66)\[ R_{D,i}=k_{D,i}\Gamma_i=A_ie^{\frac{-E_i}{RT}}\Gamma_i \]

where \(E_i\) is the adsorption energy. Denoting with \(E_0\) the adsorption energy on a free adsorption site, the adsorption energy on all successive layers is \(E_2=E_3=...E_n=\lambda\), where \(\lambda\) is the condensation enthalpy.

Following the same criterion also the adsorption constant \(k_{A,i}\), and the pre-exponential factor of the desorption constant \(A_i\) are independent from the layer index - except for those related to the adsorption on a free surface and the desorption from the first layer:

(67)\[ A_{i\geq2}=const=A \]

(68)\[ k_{A,i\geq1}=const=k_A \]

Having defined the rates of adsorption and desorption one can write population balances for every layer of the adsorbed phase. In the following \(\Gamma_0\) represents the fraction of free adsorption sites, \(\Gamma_i\) represents the fractional occupation of the \(i^{th}\) layer.

(69)\[\begin{split} \begin{cases} \frac{d\Gamma_0}{dt}&=-k_{A,0}\Gamma_0P +k_{D,1}\Gamma_1 \\ \frac{d\Gamma_1}{dt}&=+k_{A,0}\Gamma_0P -k_{D,1}\Gamma_1-k_{A,1}\Gamma_1P+k_{D,2}\Gamma_2 \\ \frac{d\Gamma_2}{dt}&=+k_{A,1}\Gamma_1P -k_{D,2}\Gamma_2-k_{A,2}\Gamma_2P+k_{D,3}\Gamma_3 \\ \vdots \\ \frac{d\Gamma_n}{dt}&=+k_{A,n-1}\Gamma_{n-1}P -k_{D,n}\Gamma_n-k_{A,n}\Gamma_nP+k_{D,n+1}\Gamma_{n+1} \\ \vdots\\ \end{cases} \end{split}\]

At equilibrium the balances reduce to:

(70)\[\begin{split} \begin{cases} 0=-k_{A,0}\Gamma_0P +k_{D,1}\Gamma_1 \\ 0=+k_{A,0}\Gamma_0P -k_{D,1}\Gamma_1-k_{A,1}\Gamma_1P+k_{D,2}\Gamma_2 \\ 0=+k_{A,1}\Gamma_1P -k_{D,2}\Gamma_2-k_{A,2}\Gamma_2P+k_{D,3}\Gamma_3 \\ \vdots \\ 0=+k_{A,n-1}\Gamma_{n-1}P -k_{D,n}\Gamma_n-k_{A,n}\Gamma_nP+k_{D,n+1}\Gamma_{n+1} \\ \vdots\\ \end{cases} \end{split}\]

From the steady state balance on free sites we get:

(71)\[ k_{A,0}\Gamma_0P=k_{D,1}\Gamma_1 \]

hence, inserting this equality into the balance on the fraction of sites occupied by a single layer, \(\Gamma_1\) we get:

(72)\[ k_{A,1}\Gamma_1P=k_{D,2}\Gamma_2 \]

Introducing the Arrhenius expression for the adsorption rates we get:

(73)\[ \Gamma_1=\frac{k_{A,0}}{k_{D,1}}\Gamma_0P=\frac{k_{A,0}}{A_{1}}e^{\frac{E_1}{RT}}P\Gamma_0 \]

and analogously for \(\Gamma_2\):

(74)\[ \Gamma_2=\frac{k_{A,1}}{k_{D,2}}\Gamma_1P=\frac{k_{A,1}}{A_{2}}e^{\frac{E_2}{RT}}P\Gamma_1 \]

a similar procedure can now be followed recursively to obtain a compact expression for the fraction of sites occupied by an arbitrary number of layers \(n\). To this aim we can introduce two constants, \(\alpha\) and \(\beta\) - defined as:

(75)\[ \alpha=\frac{k_{A,0}}{A_{1}}e^{\frac{E_1}{RT}}P \]

(76)\[ \beta=\frac{k_{A}}{A}e^{\frac{\lambda}{RT}}P \]

At this point the fraction of sites occupied by \(n\) layers can be obtained as:

(77)\[ \Gamma_n=\beta\Gamma_{n-1}=\beta^2\Gamma_{n-2}=...=\beta^{n-1}\Gamma_{1}=\beta^n\frac{\alpha}{\beta}\Gamma_0 \]

Deining for the sake of compactness the constant \(B_2=\alpha/\beta\) and introducing the volume of adsorbate per unit area \(v_s^1\) one can express the total volume adsorbed as:

(78)\[ v_s=v_s^1\sum_{i=1}^n{iB_2\beta^i\Gamma_0}=v_s^1B_2\beta\sum_{i=1}^ni\beta^{i-1}=v_s^1B_2\beta\frac{d\sum_{i=1}^n\beta^{i}}{d\beta} \]

By introducing the notable result for the term \(\sum_{i=1}^n\beta^{i}\):

(79)\[ \sum_{i=1}^n\beta^{i}=\left(\frac{1-\beta^n}{1-\beta}\right)\beta \]

one gets:

(80)\[ \frac{v_s}{v_s^1}=\frac{B_2\beta}{1-\beta}\frac{\left[1-(n+1)\beta^n+n\beta^{n+1}\right]}{\left[1+(B_2-1)\beta-B_2\beta^{n+1}\right]} \label{eq:16} \]

In order to obtain the final formulation of the BET isotherm it is useful to consider the limit corresponding to macroscopic condensation, which corresponds to a buildup of an infinite number of adsorbed layers, which corresponds to \(\beta=1\). Since this condition is realised for \(P=P^o\), it can be shown that \(\beta=\frac{k_{A}}{A}e^{\frac{\lambda}{RT}}P=P/P^o\).

Introducing this equality in eq16 one gets the so called limited form of the BET isotherm:

(81)\[ \frac{v_s}{v_s^1}=\frac{B_2\left(\frac{P}{P^o}\right)}{1-\left(\frac{P}{P^o}\right)}\frac{\left[1-(n+1)\left(\frac{P}{P^o}\right)^n+n\left(\frac{P}{P^o}\right)^{n+1}\right]}{\left[1+(B_2-1)\left(\frac{P}{P^o}\right)-B_2\left(\frac{P}{P^o}\right)^{n+1}\right]} \]

note that the left hand side of this equation can be expressed in terms of unit mass of adsorbent, instead of unit surface.

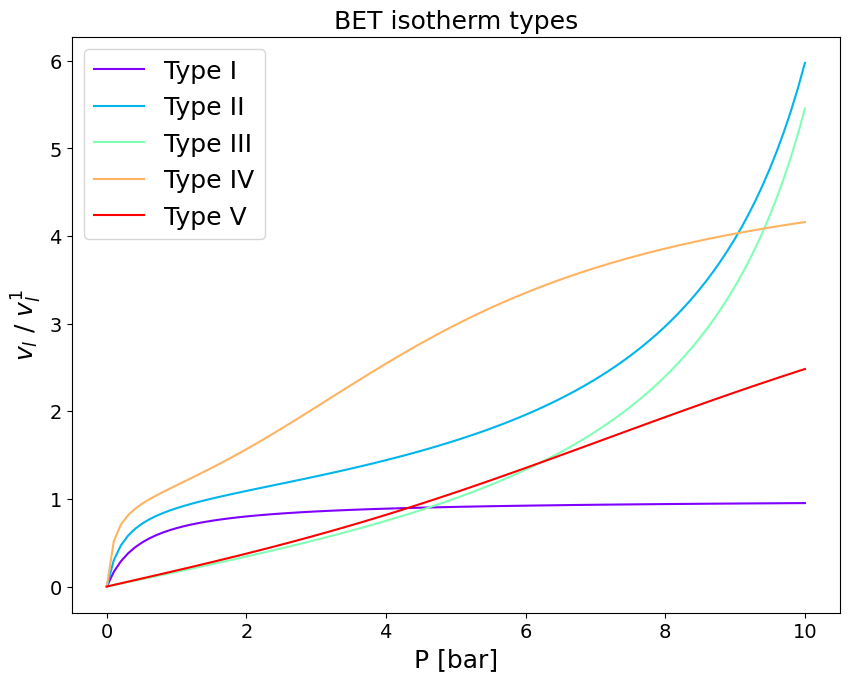
6.1 Many isotherm shapes from the same expression

Depending on the parameters introduced in the BET isotherm its functional form can adapt to capture all known shapes of adsorption isotherm. In the following we shall demonstrate combination of parameters that produce isotherms belonging to all five of the classes introduced by Brunauer (Brunauer et al. JACS 1940).

import numpy as np
import matplotlib.pyplot as plt 
from matplotlib.pyplot import cm

#Plotting
figure=plt.figure()
axes = figure.add_axes([0.1,0.1,1.2,1.2])
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)

N=100;

#Parameters
P0 = np.array([5, 12, 12, 5, 11, 11]);
B2 = np.array([10, 50, 2, 50, 2]);
n  = np.array([1,500, 500, 5, 5]);

P = np.linspace(0, 10, N)
vv1 = np.zeros(np.size(P))
   


color=iter(cm.rainbow(np.linspace(0,1,np.size(B2))))

for i in range(0,np.size(B2)):     
    S=P/P0[i]
    c=next(color)
    
    #Langmuir isotherm   
    vv1=B2[i]*S/(1-S)*(1-(n[i]+1)*np.power(S,n[i])+n[i]*np.power(S,n[i]+1))/(1+(B2[i]-1)*S-B2[i]*np.power(S,n[i]+1));
    
    axes.plot(P,vv1, marker=' ' , c=c)

    
plt.title('BET isotherm types', fontsize=18);
axes.set_xlabel('P [bar]', fontsize=18);
axes.set_ylabel('$v_l$ / $v_l^1$',fontsize=18);
axes.legend(['Type I','Type II','Type III','Type IV','Type V'], fontsize=18);