Week 2 Exercise 1: Water and Ice equilibria with vapour

Example application

Q1 Compute the VLE and SLE equilibrium lines, and the conditions in the T/P phase diagram where water vapour is in equilirbium simultaneously with ice and liquid water:

\(\Delta{h}_{ev}\)= 40.657 kJ/mol

\(\Delta{h}_{sub}\)= 54.153 kJ/mol

\(P^\circ(373 K)\)=101300 Pa

\(P^s(273 K)\)=611.153 Pa

Q2 Demonstrate that the conditions defining the T and P where water vapour is in equilirbium simultaneously with ice and liquid water correspond to the triple point.

Example solution Q1

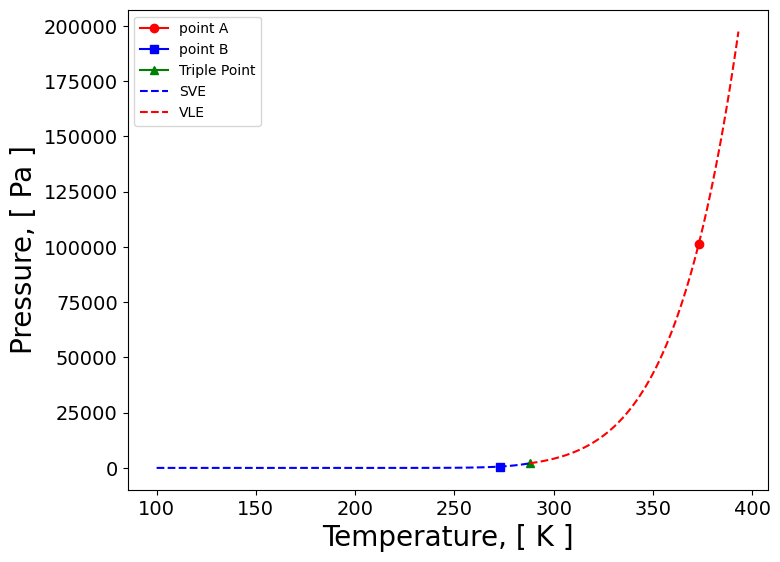
import numpy as np
import matplotlib.pyplot as plt 

TA = 373 # K
TB = 273 # K

R = 8.314E-3 # kJ/mol

PoA=101300 # Pa
Dhev=40.657 # kJ/mol
PoB=611.153 # kJ/mol 
Dhsub=54.153 # kJ/mol 

C_evaporation = np.log(PoA) + Dhev/(R*TA)
C_sublimation = np.log(PoB) + Dhsub/(R*TB)

T_triple=(Dhsub-Dhev)/R/(C_sublimation-C_evaporation)
P_triple = np.exp(-Dhsub/(R*T_triple)+C_sublimation)

figure=plt.figure()
axes = figure.add_axes([0.1,0.1,1.,1.])
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)

axes.plot(TA,PoA,'r-o',label='point A')
axes.plot(TB,PoB,'b-s',label='point B')
axes.plot(T_triple,P_triple,'g-^',label='Triple Point')

T1=np.linspace(100,T_triple,100)
T2=np.linspace(T_triple,TA+20,100)

Pv_T=np.exp(-Dhev/(R*T2)+C_evaporation)
Ps_T=np.exp(-Dhsub/(R*T1)+C_sublimation)

axes.plot(T1,Ps_T,'b--',label='SVE')
axes.plot(T2,Pv_T,'r--',label='VLE')

axes.legend()
axes.set_xlabel('Temperature, [ K ]',fontsize=20)
axes.set_ylabel('Pressure, [ Pa ]',fontsize=20)

#axes.set_yscale('log')

print("C_ev: ",C_evaporation,"\nC_sub: ",C_sublimation)
print("T_triple: ",T_triple," K")
print("P_triple: ",P_triple," Pa")

C_ev:  24.63625785574074 
C_sub:  30.274216396724825
T_triple:  287.92088692645035  K
P_triple:  2104.3931734818325  Pa