Week 2 Exercise: Liquid Vapour Equilibria

Bubble and Dew points

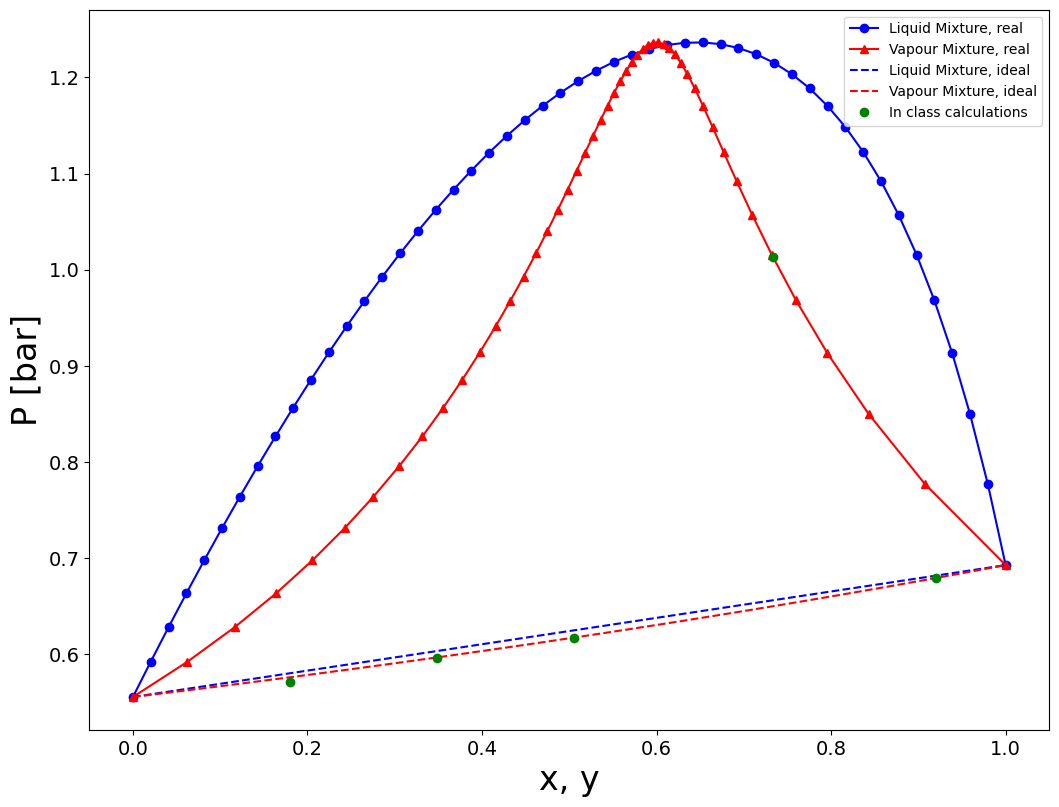
Compute the bubble and dew pressure for a chloroform-methanol mixture at 50\(^\circ\) C for all possible molar compositions.

Data and useful information

The Equilibrium vapour pressure in bar is given by the following Antoine equation:

\[ \log_{10}{P^\circ(T)}= A-\frac{B}{T+C} - \log_{10}750 \]

with (chloroform=1, methanol=2):

\(A=[6.95465, 8.08097]\)

\(B=[1170.966, 1582.271]\)

\(C=[226.232, 239.726]\)

The activity of the components of the mixture (chloroform=1, methanol=2) can be described by the Van Laar model i.e.:

\[ \ln{\gamma_1}=\frac{A_{12}}{1+\frac{A_{12}x_1}{A_{21}x_2}} \]

\[ \ln{\gamma_2}=\frac{A_{21}}{1+\frac{A_{21}x_2}{A_{12}x_1}} \]

with \(A_{12}=0.9726\) and \(A_{21}=1.9210\).

Problem definitions:

When computing the Bubble pressure, we are estimating the pressure (and the composition) of the very first bubble of vapour formed in a liquid at known composition (\(\mathbf{x}\) is known). The equations we can use to solve the problem are the equilibrium statements N-1 species in the system (i.e. the Raoult equation in the case of an ideal mixture of ideal gases) and the stoichiometric constraint on the composition of the vapour phase.

When computing the Dew pressure, we are estimating the pressure (and the composition) of the very first droplet of liquid formed in a vapour at known composition (\(\mathbf{y}\) is known). The equations we can use to solve the problem are the equilibrium statements N-1 species in the system (i.e. the Raoult equation in the case of an ideal mixture of ideal gases) and the stoichiometric constraint on the composition of the liquid phase.

from IPython.display import HTML
HTML('VLequilibrium_interactive.html')

Interactive Phase Diagram

ideal mixture -> real mixture:

Value: 0

Example solution: Bubble points

import numpy as np
import matplotlib.pyplot as plt 

T=[50]
x=np.linspace(0,1,50)

AA=np.array([6.95465, 8.08097])
AB=np.array([1170.966, 1582.271])
AC=np.array([226.232, 239.726])

VLA12=0.9726
VLA21=1.9210

xinclass=np.array([0.15, 0.3, 0.45,  0.9, 0.9])
yinclass=np.array([0.18, 0.349, 0.505,  0.92, 0.734])
Pinclass=np.array([0.571, 0.596, 0.617, 0.679, 1.013])

gamma1=np.exp(VLA12/(1+VLA12*x/(VLA21*(1-x))))
gamma2=np.exp(VLA21/(1+VLA21*(1-x)/(VLA12*(x))))

Peq=(10**((AA-AB/(T+AC))))/750 #bar

Pbubble=Peq[0]*x*gamma1+Peq[1]*(1-x)*gamma2
K1=(Peq[0]*gamma1)/Pbubble
K2=(Peq[1]*gamma2)/Pbubble
ybubble=K1*x

Pbubble_ideal=Peq[0]*x+Peq[1]*(1-x)

ybubble_ideal=Peq[0]/Pbubble_ideal*x

figure=plt.figure()
axes = figure.add_axes([0.1,0.1,1.5,1.5])
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)

axes.plot(x,Pbubble,'b-o',label='Liquid Mixture, real')
axes.plot(ybubble,Pbubble,'r-^',label='Vapour Mixture, real')


axes.plot(x,Pbubble_ideal,'b--', label='Liquid Mixture, ideal')
axes.plot(ybubble_ideal,Pbubble_ideal,'r--',label='Vapour Mixture, ideal')

axes.plot(yinclass,Pinclass,'go',label='In class calculations')

axes.set_xlabel('x, y', fontsize=24);
axes.set_ylabel('P [bar]',fontsize=24); 

axes.legend();

/var/folders/4v/jxb311rn5nq2q59y91zzgxd40000gp/T/ipykernel_85285/1455094392.py:18: RuntimeWarning: divide by zero encountered in divide
  gamma1=np.exp(VLA12/(1+VLA12*x/(VLA21*(1-x))))
/var/folders/4v/jxb311rn5nq2q59y91zzgxd40000gp/T/ipykernel_85285/1455094392.py:19: RuntimeWarning: divide by zero encountered in divide
  gamma2=np.exp(VLA21/(1+VLA21*(1-x)/(VLA12*(x))))